¿Cómo realizamos regla de tres en Excel?

Regla de tres:

Es una operación que nos ayuda a resolver problemas de proporcionalidad.

Para efectuar esta operación se necesita tres datos: dos magnitudes proporcinoales entre sí, y una magnitud adicional. A partir de estos, se calcula el cuarto término de la proporcionalidad.

Existen dos tipos de porporcionalidades a las cuales se puede aplicar la regla de tres: Directa e Inversamente Proporcional.

Ejemplos:

1. Una universidad requiere conocer el porcentaje en el que aumentó o disminuyó la cantidad de alumnos este año en comparación al año pasado. Para ello se tiene las cantidades de alumnado de ambos años.

Este es un problema de proporcionalidad directa.

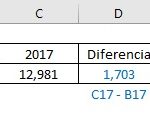
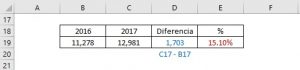
La cantidad de alumnos aumentó en 1,703 en comparación al año pasado. Ahora se usará la regla de tres para hallar el porcentaje en que aumentó.

Por la tanto la cantidad de alumnos aumentó en 15.10%.

2. En un refugio se tiene alimento suficiente para abastecer a 5,000 personas durantes 45 días. Desean saber cuántos días duraría la misma cantidad de alimento si el número de refugiados aumenta a 6,500 personas.

Este es un problema de proporcionalidad inversa, por lo que el cálculo es diferente.

Después de aplicar la regla de tres se concluye que el alimento durará 34.62 días para 6,500 personas.

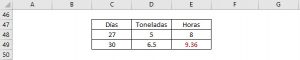
3. Una fábrica de harina de pescado demora 27 días en producir 5 toneladas de sacos de harina de pescado cumpliendo una jornada de 8 horas diarias. La fábrica quiere saber cuántas horas extras por día necesitará para cumplir una orden de 6.5 toneladas de sacos de harina en 30 días.

Colocando los datos en una tabla:

Analizando las proporcionalidades de los datos:

Efectuando la regla de tres:

Calculando:

Por lo tanto, para producir 6.5 toneladas de sacos de harina de pescado en 30 días se necesitarán 1.36 horas extras diarias.